Chaos Theory and Simulating a Chaotic System

 

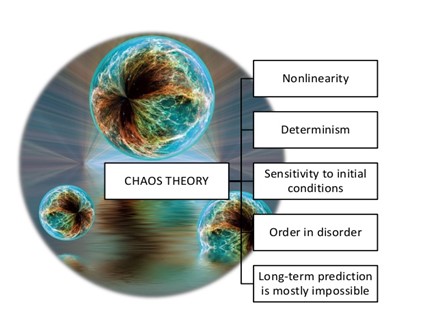
 WHAT IS CHAOS THEORY?  

 

“As far as the laws of mathematics refer to reality, they are not certain, and as far as they are certain, they do not refer to reality.”

-Albert Einstein

 

Chaos is the science of surprises, of the nonlinear and the unpredictable. It teaches us to expect the unexpected.

 While most traditional science deals with supposedly predictable phenomena like gravity, electricity, or chemical reactions, Chaos Theory deals with nonlinear things that are effectively impossible to predict or control, like turbulence, weather, the stock market, our brain states, and so on. 

These phenomena are often described by fractal mathematics, which captures the infinite complexity of nature. Many natural objects exhibit fractal properties, including landscapes, clouds, trees, organs, rivers etc, and many of the systems in which we live exhibit complex, chaotic behavior.

 Recognizing the chaotic, fractal nature of our world can give us new insight, power, and wisdom. For example, by understanding the complex, chaotic dynamics of the atmosphere, a balloon pilot can “steer” a balloon to a desired location. By understanding that our ecosystems, our social systems, and our economic systems are interconnected, we can hope to avoid actions which may end up being detrimental to our long-term well-being.

 

Chaos Theory

Chaotic systems are unstable since they tend not to resist any outside disturbances but instead react in significant ways. The Chaotic Systems can be classified in two types:

1.      Dynamic systems: Simplified model for the time-varying behaviour of an actual system.      These systems are described using differential equations specifying the rates of change for each variable.  

2.      Deterministic systems: System in which no randomness is involved in the development of future states of the system. This property implies that two trajectories emerging from two different close-by initial conditions separate exponentially over time. Chaotic systems are unstable since they tend not to resist any outside disturbances but instead react in significant ways.

 

Attractive, strange behaviour:

First, a highly regular motion_ towards the attractor … then a much more irregular motion on _it. - Ian Stewart, The Magical Maze.

 

Stability is desirable in many scenarios, such as flying. Commercial aircraft are aerodynamically stable, so that a small turbulent nudge (possibly butterfly-related) won’t push the plane out of a level flightpath.

Comfortingly, it takes a large change in the flight controls to effect a large change in the plane’s motion.

On the other hand, this stability is somewhat of an inconvenience to fighter pilots who prefer their aircraft to make rapid changes with minimal effort.

Lorenz Attractor

Modern fighter jets achieve great manoeuvrability by virtue of being aerodynamically unstable - the slightest nudge is enough to drastically alter their flightpath.

If you can tease out the pattern’s underlying chaotic systems, you can effect a measure of control over randomness and turn instability into an asset.

The key to unlocking the hidden structure of a chaotic system is in determining its preferred set of behaviours - known to mathematicians as its attractor.

Imagine taking a ping-pong ball far out into the ocean and letting it go. If released above the water it will fall, and if released underwater it will float.

No matter where it starts, the ball will immediately move in a very predictable way towards its attractor - the ocean surface. Once there it clings to its attractor as it is buffeted to and fro in a literal sea of chaos, and quickly moves back to the surface if temporarily thrown above or dumped below the waves.

Though we may not be able to predict exactly how a chaotic system will behave moment to moment, knowing the attractor allows us to narrow down the possibilities.

It also allows us to accurately predict how the system will respond if it is jolted off its attractor.

 

TYPES OF ATTRACTORS:

1.      Point attractor: There is only one outcome for the system. Death is a point attractor for living things.

2.       Limit cycle or Periodic Attractor: Instead of moving to a single state as in a point attractor, the system settles into a cycle.

3.      Strange Attractor or Chaotic Attractor: double spiral which never repeats itself. Strange attractors are shapes with fractional dimension; they are fractals.  

 

FRACTALS:

 A fractal is a never-ending pattern. Fractals are infinitely complex patterns that are self-similar across different scales. They are created by repeating a simple process over and over in an ongoing feedback loop. Driven by recursion, fractals are images of dynamic systems – the pictures of Chaos. Geometrically, they exist in between our familiar dimensions. Fractal patterns are extremely familiar, since nature is full of fractals. For instance: trees, rivers, coastlines, mountains, clouds, seashells, hurricanes, etc.

Fractals

 

THE MATHEMATICS BEHIND BUTTERFLY EFFECT:

Tiny variations … never repeat, and vastly affect the outcome. - Jeff Goldblum (“Ian Malcolm”), Jurassic Park.

 

In 1961, a meteorologist by the name of Edward Lorenz made a profound discovery.

Lorenz was utilising the new-found power of computers in an attempt to more accurately predict the weather. He created a mathematical model which, when supplied with a set of numbers representing the current weather, could predict the weather a few minutes in advance.

One day, Lorenz decided to rerun one of his forecasts. In the interests of saving time he decided not to start from scratch; instead he took the computer’s prediction from halfway through the first run and used that as the starting point.

After a well-earned coffee break, he returned to discover something unexpected. Although the computer’s new predictions started out the same as before, the two sets of predictions soon began diverging drastically. What had gone wrong?

Lorenz soon realised that while the computer was printing out the predictions to three decimal places, it was actually crunching the numbers internally using six decimal places.

A difference of one part in a thousand: the same sort of difference that a flap of a butterfly’s wing might make to the breeze on your face. The starting weather conditions had been virtually identical. The two predictions were anything but.

Lorenz had found the seeds of chaos. In systems that behave nicely - without chaotic effects - small differences only produce small effects. In this case, Lorenz’s equations were causing errors to steadily grow over time.

This meant that tiny errors in the measurement of the current weather would not stay tiny, but relentlessly increased in size each time they were fed back into the computer until they had completely swamped the predictions.

Lorenz famously illustrated this effect with the analogy of a butterfly flapping its wings and thereby causing the formation of a hurricane half a world away.

 

The Butterfly Effect

 

SIMULATION:-

 

 Simulating the Double Pendulum.

In physics and mathematics, in the area of dynamical systems, a double pendulum is a pendulum with another pendulum attached to its end, and is a simple physical system that exhibits rich dynamic behavior with a strong sensitivity to initial conditions.

The motion of a double pendulum is governed by a set of coupled ordinary differential equations and is chaotic.

 

Several variants of the double pendulum may be considered; the two limbs may be of equal or unequal lengths and masses, they may be simple pendulums or compound pendulums (also called complex pendulums) and the motion may be in three dimensions or restricted to the vertical plane. In the following analysis, the limbs are taken to be identical compound pendulums of length l and mass m, and the motion is restricted to two dimensions.

Schematic Diagram of Double Pendulum

 

CODE SNIPPET:

 

Code Snippet

Code

 

RESULTS:

The double pendulum undergoes chaotic motion, and shows a sensitive dependence on initial conditions. The image to the below shows the amount of elapsed time before the pendulum flips over, as a function of initial position when released at rest. Here, the initial value of θ₁ ranges along the x-direction from −π to π. The initial value θ₂ ranges along the y-direction, from −π to π. The colour of each pixel indicates whether either pendulum flips within:

·         √^l⁄_g (black)

·         10√^l⁄_g (red)

·         100√^l⁄_g (green)

·         1000√^l⁄_g (blue) or

·         10000√^l⁄_g (purple).

 

Initial conditions that do not lead to a flip within 10000√^l⁄_g are plotted white.

Graph Plot of Motion of Double Pendulum

The x and y directions represents the angles that a double pendulum consisting of two uniform bars of same length and mass makes with the vertical direction, being the center of the image 0º and the extremities +- 179.9º. Both bars are initially with zero velocity. The color represents the time (in units of ) that it takes for one of the two pendulums to flip, being black less than 1 unit of time, from red to violet it ranges in a logarithm scale from 1 to 10000 units of time. White means no flip was observed within 10000 units of time. 

 

   Simulation of path of Double Pendulum

 

Long Exposure shot of Double Pendulum

 

 

CONCLUSION: 

Everything in the universe is under the control of Chaos Theory. Irregularity leads to complex solutions. 

Chaos theory is a new way of thinking about what we have. It gives us a new concept of measurements and scales. It looks at the universe in an entirely different way. Understanding chaos understands life as we know it. Because of chaos, it is realized that even simple systems may give rise to and, hence, be used as models for complex behavior.

 Chaos forms a bridge between different fields. Chaos offers a fresh way to proceed with observational data, especially those data which may be ignored because they proved too erratic. The specificity of present time physics, with entropy, chaos, and fractal dimensions, confers reality to phenomena as we can perceive and measure them, and it somehow invalidates the idea of a fundamental, or true, reality that might be explained by an elegant model.

 The use of such models entails too many simplifications, and may lead for instance to the reversibility of time that is imposed by the mathematical structure of mechanics. More research should be conducted on that field in order to find out how to control the chaotic behavior of different systems in order to increase the validity of our future models and plans especially in the field of economics, where future models and plans can give crucial information about the general state of the economy in different countries.

 In this blog, some basic parts of chaotic systems have been explored. Recently extensive research works in various other fields of mathematics have been going only to better understand these chaotic systems.